[C++] 완전탐색과 백트래킹

썸네일

완전탐색이란?

완전탐색은 모든 경우의 수를 탐색하는 알고리즘이다. 무식하게 한다는 의미로 브루트포스(Brute Force) 알고리즘이라고도 부른다.

직관적이기 때문에 이해하기 쉬우며 문제의 정확한 결과를 얻어낼 수 있는 가장 확실하며 기초적인 방법이다.

 

모든 경우의 수를 탐색하는 것은 저번 포스트의 순열이나 조합을 사용하거나, 단순 구현을 하면 된다.

하지만 시간 초과가 날 수 있으므로, 보통은 최대 범위가 1억 미만일 때까지만 한다.

 

완전탐색으로 문제 푸는 방법

완전탐색을 활용할 때 가장 간단한 방법은 반복문(for, while)을 활용하는 것이다.

 

만약 반복문만 사용하는 것이 너무 복잡하거나 특정 행위를 반복하며 매개변수만 변경하면 될 것 같은 경우에는 재귀함수를 사용할 수 있다.

ex. 조합/순열 + (DFS, BFS 등 알고리즘), 경우의 수마다 생각해야 하는 로직이 있을 경우

 

백트래킹

백트래킹은 해를 찾는 도중 막히면 더 이상 깊이 들어가지 않고, 이전 단계로 되돌아가서 해를 찾아나가는 기법이다.

쉽게 말해, 완전탐색에 가지치기를 추가하여 불필요한 경우의 수를 제외하고 생각하는 알고리즘이다.

 

출처: https://pythonwife.com/backtracking-in-python/

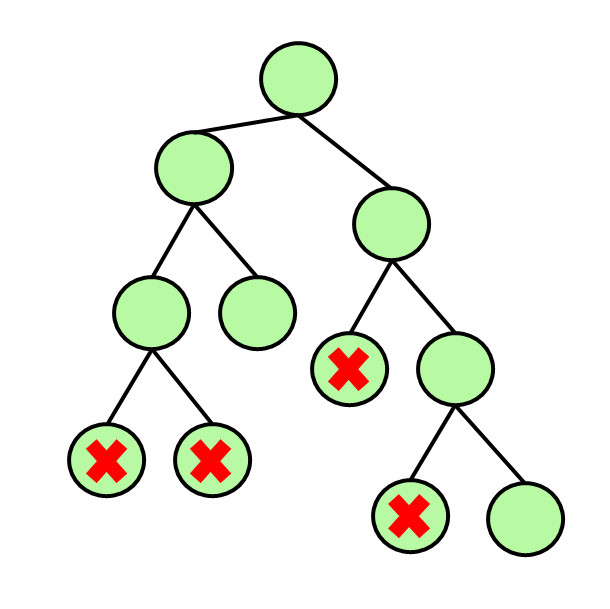
위 사진에서, X표가 쳐진 노드는 문제의 조건을 충족하지 못한 노드로 더 이상 depth가 깊이 들어가지 않는 것을 볼 수 있다. 이렇게 막히면 더 이상 깊이 들어가지 않는다. 또는, 문제 조건에 맞는 해답을 찾았을 때 나머지 경우의 수를 확인하지 않고 바로 return하는 것도 가능하다.

 

완전탐색을 할 때는 원상복구를 잘하자!

14502번: 연구소

14502번 문제로 예시를 들어보겠다. (스포주의)

해당 문제에서는 새로운 벽(1)을 3개 세운 뒤 바이러스(2)가 얼마나 퍼지는지 세는 문제이다. (엄밀히 말하면 안전 영역인데 설명의 편의상)

초록색으로 표시된 1이 새로 세운 벽을 의미한다. 위 사진은 경우의 수 중 하나로, 다음 경우의 수를 탐색할 때는 초록색 1 중 하나를 허물고 새로운 자리(0)에 벽(1)을 세워야 한다.

 

이 때 벽을 허무는 행위는 상태값이 그 다음 경우의 수에 반영되지 않도록 하는 행위이다.

 

저번 포스트에서 재귀로 순열이나 조합을 구현할 때, 재귀 코드 다음 줄에 swap이나 pop_back 함수가 있던 것이 원상 복구를 위해서였다.

void makePermutation(int n, int r, int depth) {
    cout << "n: " << n << ", r: " << r << ", depth: " << depth << "\n";

    if (r == depth) {
        printV(v);
        return;
    }


    for (int i = depth; i < n; ++i) {
        swap(v[i], v[depth]);
        makePermutation(n, r, depth + 1);
        swap(v[i], v[depth]);
    }
}

 

Reference

10주완성 C++ 코딩테스트 | 알고리즘 코딩테스트 - 인프런 | 강의