반응형
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
1. 문제 설명

2. 구현 아이디어 1 - 맞았습니다!!
별다른 아아디어 없이, MST 알고리즘을 적용하면 풀 수 있는 문제이다.
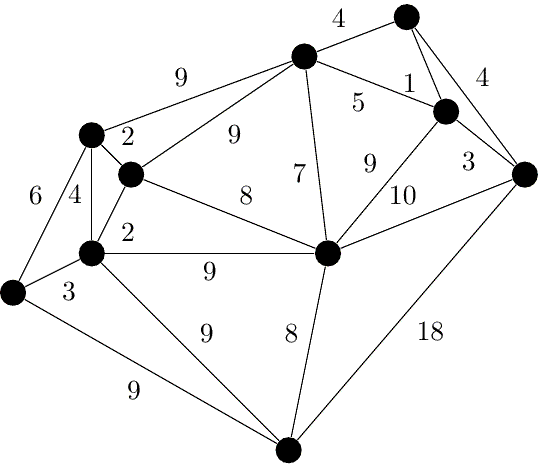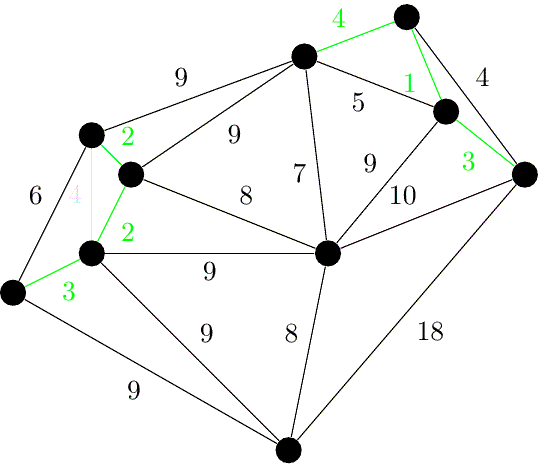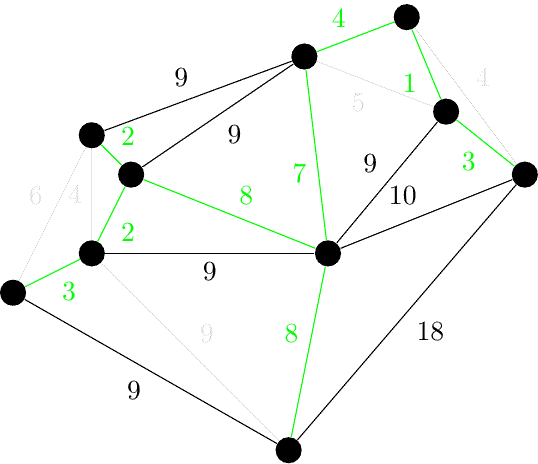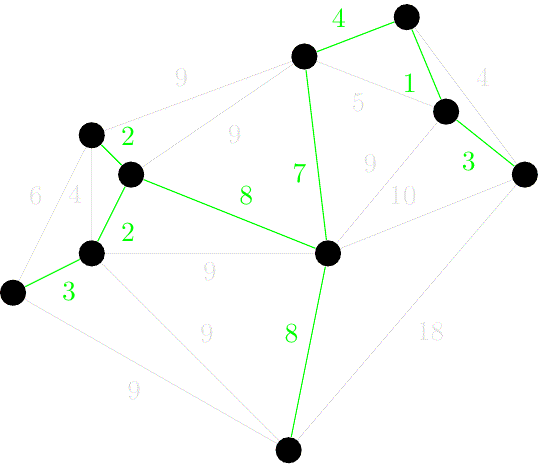
최소 신장 트리(MST, Minimum Spanning Tree) - 크루스칼, 프림 알고리즘
1. 최소 신장 트리란? 신장 트리(Spanning Tree)란 그래프의 모든 노드가 사이클 없이 연결된 부분 그래프를 의미한다. 신장 트리는 여러 개가 존재할 수 있으며, 이 중 모든 노드가 최소 간선의 합으
leeeeeyeon-dev.tistory.com
이전 포스트에서 MST 알고리즘을 정리해보았으니, 이번에는 직접 구현해보자.
이번 문제에서는 정점이 최대 10,000개이고 간선이 최대 100,000개이다. Worst Case의 경우 정점 대비 간선의 수가 많은 Dense Graph이므로 크루스칼 알고리즘을 사용하는 것이 적합하다.
#include <bits/stdc++.h>
using namespace std;
int parent[10'001];
int find(int x) {
if (x==parent[x]) return x;
int p = find(parent[x]);
parent[x] = p;
return parent[x];
}
void merge(int a, int b) {
int A = find(a);
int B = find(b);
if (A < B) parent[B] = A;
else parent[A] = B;
}
// 두 노드를 연결했을 때 루트 노드가 같다면
// 사이클이 형성됨
bool isCycle(int a, int b) {
int A = find(a);
int B = find(b);
if (A == B) return true;
return false;
}
int main(int argc, char** argv)
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int v, e, a, b, c;
cin >> v >> e;
vector<pair<int, pair<int, int>>> graph = vector<pair<int, pair<int, int>>>();
// parent 배열 초기화
for (int i = 1; i <= v; ++i) {
parent[i] = i;
}
for (int i = 0; i < e; ++i) {
cin >> a >> b >> c; // a와 b 정점을 가중치 c로 잇는다
graph.push_back({c, {a, b}});
}
// 첫 번째 원소인 간선을 기준으로 정렬됨
sort(graph.begin(), graph.end());
// c의 범위가 INT_MIN~INT_MAX이므로 가중치를 더하다 보면
// int의 범위를 넘을 수 있음
long long sum = 0;
for (auto elem : graph) {
// 사이클이 형성되지 않을 경우에만 간선 연결
if (!isCycle(elem.second.first, elem.second.second)) {
sum += elem.first;
merge(elem.second.first, elem.second.second);
}
}
cout << sum << "\n";
return 0;
}

반응형