[Programmers] 유사 칸토어 비트열
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
1. 문제 설명
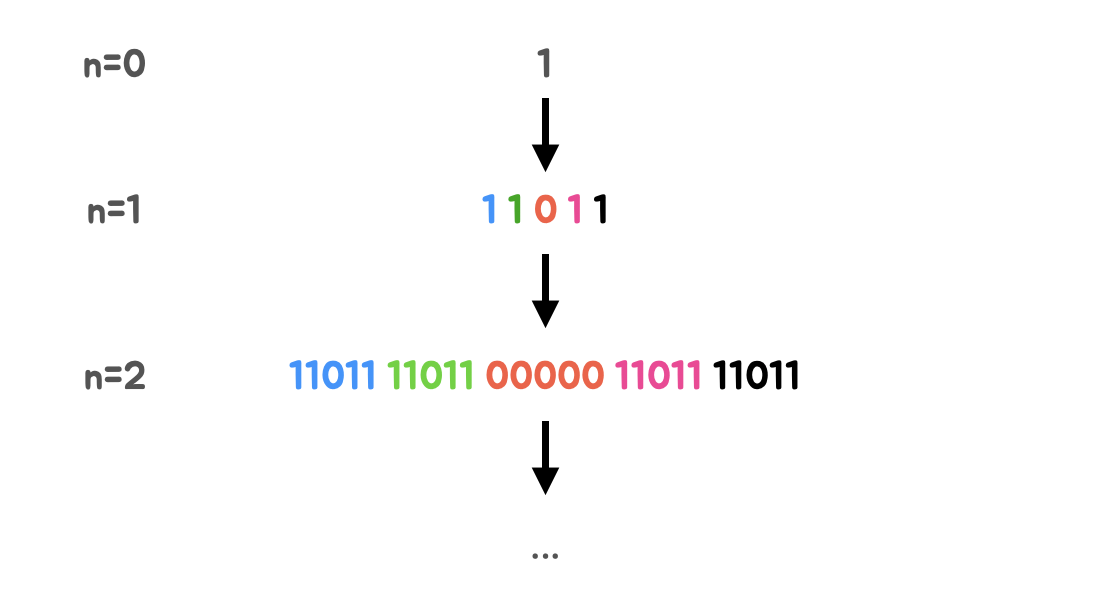
- 0번째 유사 칸토어 비트열은 "1"
- n번째 유사 칸토어 비트열은 n-1번째 유사 칸토어 비트열에서
- 1을 11011로 치환
- 0을 00000로 치환
n, l, r이 주어졌을 때 n번째 유사 칸토열에서 [l, r] 구간에서의 1의 개수를 반환해야 한다.
더 자세한 문제 설명이 필요하다면 위 링크 참고 ...
2. 구현 아이디어1 - 틀렸습니다
처음에 백준 4779번 칸토어 집합 문제가 떠올라서 재귀를 사용해서 문제에 주어진 내용을 그대로 구현하였다.
#include <string>
using namespace std;
typedef long long ll;
int ret;
ll L, R;
// 구간 내 1의 개수를 count
int countOne(string s) {
int cnt = 0;
for(int i = L-1; i < R; i++) {
if (s[i] == '1') cnt++;
}
return cnt;
}
void makeCantor(int n, int cur, string s) {
// 재귀 탈출
if (cur == n) {
ret = countOne(s);
return;
}
string ns = "";
for (int i = 0; i < s.length(); i++) {
if (s[i] == '1') ns += "11011";
else ns += "00000";
}
makeCantor(n, cur + 1, ns);
}
int solution(int n, ll l, ll r) {
L = l;
R = r;
makeCantor(n, 0, "1");
return ret;
}
하지만 시간 초과가 발생하였다!

정확히 연산 양을 계산하진 않았지만 제한사항이 매우 크고 재귀까지 했으니 시간 초과 날 만두 ...
3. 구현 아이디어2 - 정답입니다!
재귀를 좀 더 효율적으로 해야 할 것 같아 유사 칸토어 비트열의 규칙을 찾아보았다.
- K번째 유사 칸토어 비트열의 길이 = 5^k
- K번째 유사 칸토어 비트열을 5등분하면 3번째 구간은 무조건 0으로만 구성되어있음
위 규칙을 사용하여 l과 r이 5등분했을 때 어느 구간에 속하는지 계산하면 되지 않을까?했는데 경우의 수가 많고 복잡한 것 같아 다른 사람의 풀이를 참고하였다.
일반적인 풀이는 내가 떠올린 것과 비슷하게 수학적인 규칙을 찾고 분할 정복 알고리즘을 문제를 푸는 것이다.
하지만 더 똑똑하고 쉬운 풀이 방법을 찾아 해당 방법을 참고하여 문제를 풀었다!
🌟 K번째 유사 칸토어 비트열에서 해당 위치가 0인 인덱스를 찾아보자
- 1 → []
- 11011 → [2]
- 1101111011000001101111011 → [2, 7, 10, 11, 12, 13, 14, 17, 22]
- …
이제 위에서 찾았던 인덱스를 5진수로 바꿔보자
- []
- [002]
- [002, 012, 020, 021, 022, 023, 024, 032, 042]
- [0002, 0012, 0020, 0021, 0022, 0023, 0024, 0032, 0042, 0120, 0121 ...]
여기서 규칙을 찾아보면 5진수로 표혔했을 때 하나라도 2가 포함되어 있으면 해당 인덱스의 값은 0이라는 것을 알 수 있다.
이것을 10진수 관점으로 말하면 인덱스 i가 5로 나눌 수 없을 때까지 계속 나눴을 때 한 번이라도 나머지가 2가 나오면 해당 인덱스 값은 0이라는 것과 동일하다.

왜냐하면 위 이진수 계산법 사진처럼 n진수는 10진수를 n으로 나눴을 때 나머지를 나열한 것이 되기 때문이다.
using namespace std;
typedef long long ll;
// 인덱스 x를 5로 나눌 수 없을 때까지 계속 나누면서 나머지가 2가 나오는지 확인
bool isOne(ll x) {
while (x >= 5) {
// 해당 인덱스의 수는 0
if (x % 5 == 2) return false;
x /= 5;
}
return x != 2;
}
int solution(int n, ll l, ll r) {
int answer = 0; // 값이 1인 인덱스 수
for (ll i = l-1; i < r; i++) {
if (isOne(i)) answer++;
}
return answer;
}
5진수로 문제를 바라봤다는 점과 풀이가 단순 구현으로 엄청 간단해졌다는 점에서 감탄스러운 풀이였다.