[C++] 순열과 조합
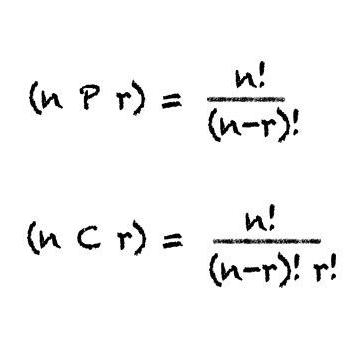
순열 vs 조합
- 순서와 상관 있이 뽑는 경우 > 순열
- 순서와 상관 없이 뽑는 경우 > 조합
- 순서를 재배치하여 ~~~한 순서의 경우 최대값을 구하는 문제 > 순열
1, 2, 3에서 3개를 뽑을 때
- 순열 - {1, 2, 3}
- 조합 - {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}
next_permutation
C++에서는 next_permutation이라는 함수를 제공하고 있다.
bool next_permutation (BidirectionalIterator first, BidirectionalIterator last);next_permutation에서는 매개변수로 시작 지점과 끝 지점 iterator을 받는다.
주의
끝 지점의 iterator에는 마지막 값의 "다음"을 넣어주어야 한다.
| Index | 0 | 1 | 2 |
| 원소 | 1 | 2 | 3 |
{1, 2, 3}이라는 배열이 있을 때, last=3이 되어야 한다.
next_permutation은 오름차순으로 정렬된 배열을 기반으로 순열을 만든다.
prev_permutation은 내림차순으로 순열을 만든다.
하지만, 둘 다 외울 필요 없이 next_permutation만 외우고 next_permutation으로 오름차순으로 순열을 만들고 원소를 뽑으면 된다.
코드 예시
#include <bits/stdc++.h>
using namespace std;
int main() {
int a[] = {1, 2, 3};
do {
for (int i: a) {
cout << a[i] << " ";
}
cout << "\n";
} while (next_permutation(&a[0], &a[0] + 3));
}
// 2 3 1
// 3 1 2
// 3 1 1
// 1 1 3
// 1 1 2
// 1 1 2array 대신 vector 타입을 사용할 경우 a.begin(), a.end() iterator을 매개변수로 하면 된다.
next_permutation(a.begin(), a.end())
앞서 오름차순으로 정렬된 배열을 기반으로 순열을 만든다고 했다. 진짜 그런지 직접 확인해보자.
a 배열을 {2, 1, 3}으로 변경해보자.
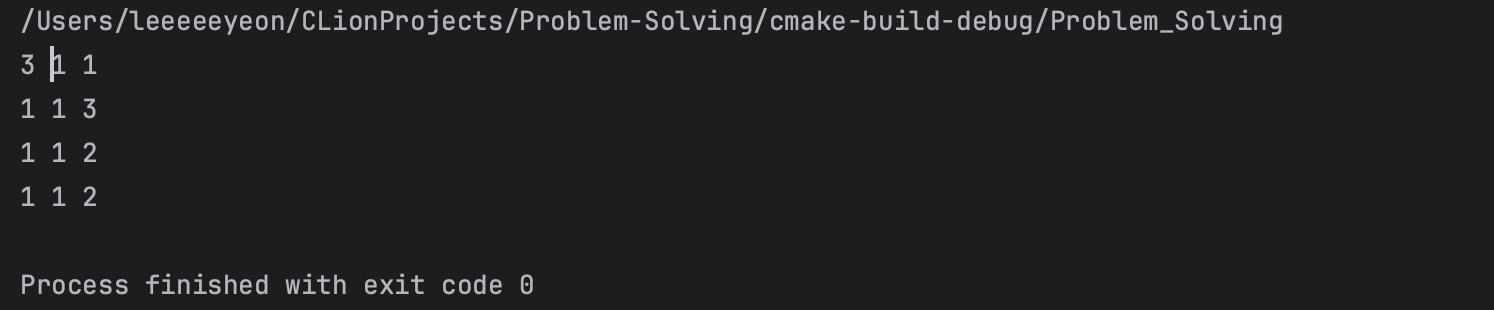
결과가 제대로 나오지 않는 것을 확인할 수 있다.
그렇기 때문에 만약 오름차순이 보장되지 않은 배열이라면, 순열을 만들기 전에 배열을 정렬해주어야 한다.
순열 공식
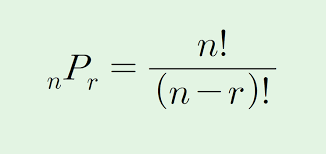
위와 같은 공식을 통해 순열의 경우의 수가 몇 개인지 구할 수 있다.
순열 직접 구현 with 재귀
이번에는 STL을 사용하지 않고 직접 구현해보자.
순열을 직접 구현할 때는 재귀를 사용할 수 있다.
#include <bits/stdc++.h>
using namespace std;
vector<int> v = {1, 2, 3};
void printV(vector<int> &v) {
for (int i = 0; i < v.size(); ++i) {
cout << v[i] << " ";
}
cout << "\n";
}
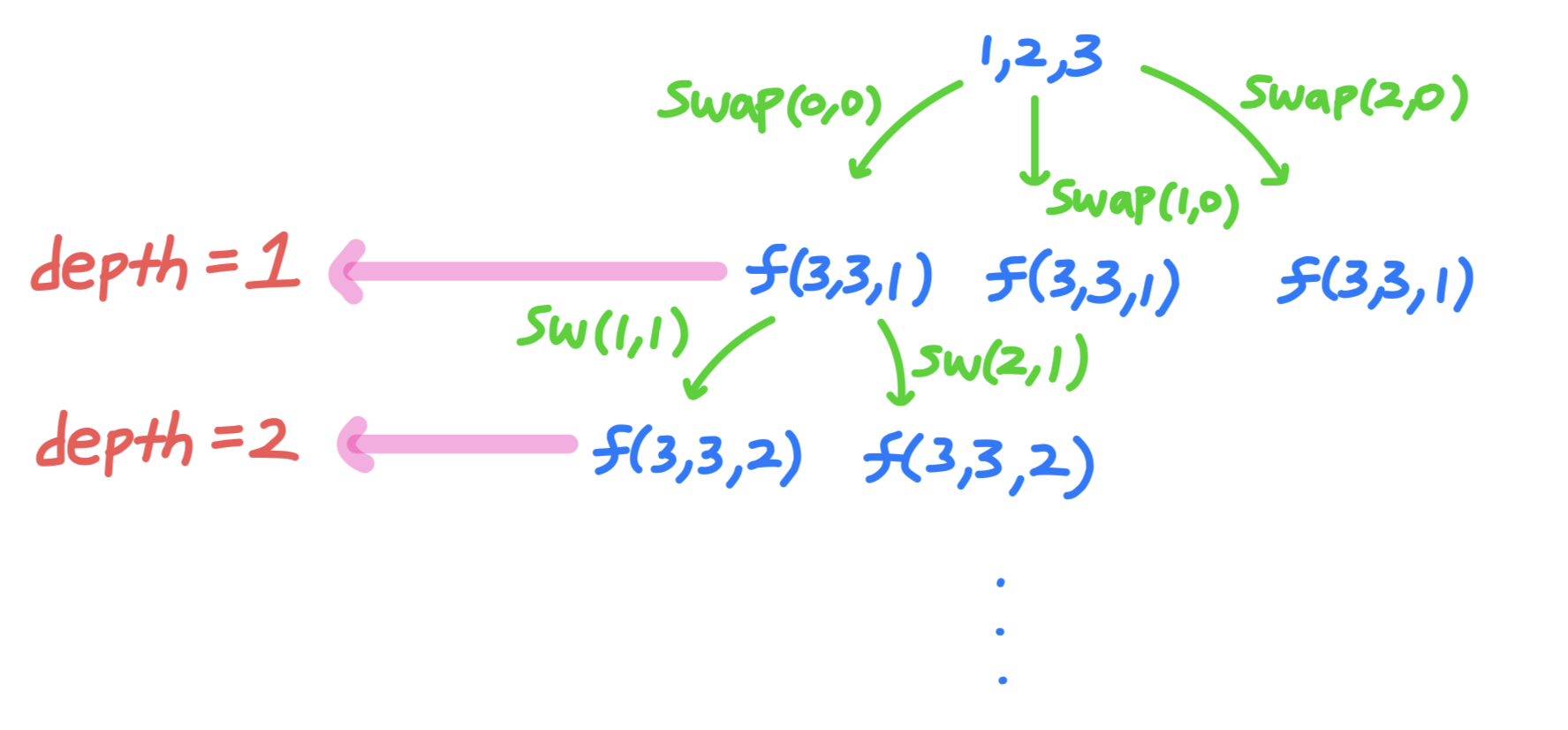
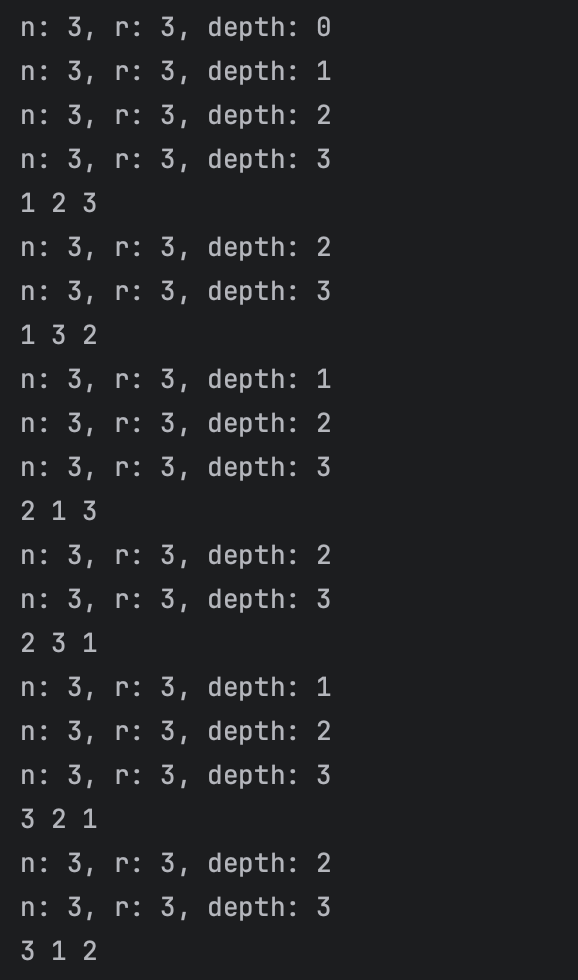
void makePermutation(int n, int r, int depth) {
cout << "n: " << n << ", r: " << r << ", depth: " << depth << "\n";
if (r == depth) {
printV(v);
return;
}
for (int i = depth; i < n; ++i) {
swap(v[i], v[depth]);
makePermutation(n, r, depth + 1);
swap(v[i], v[depth]);
}
}
int main() {
makePermutation(3, 3, 0);
}
조합
조합은 앞서 설명한 것처럼 순서가 없다. 그렇기 때문에 몇 명을 뽑을지 결정하는 문제에서 유용하게 사용할 수 있다.
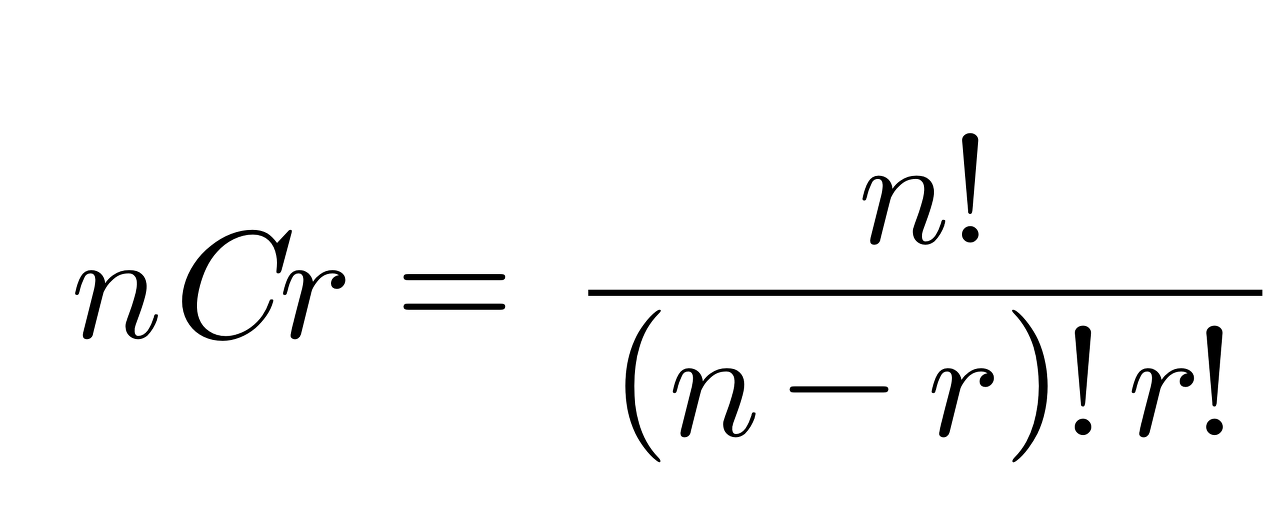
조합은 반복문이나 재귀를 사용하여 구현할 수 있는데 3개 이하는 반복문, 4개 이상일 때는 재귀를 사용하여 구현하면 좋다.
재귀로 구현
#include <bits/stdc++.h>
using namespace std;
int n = 5;
int k = 3;
vector<int> b;
void printV(vector<int> &v) {
for (int i = 0; i < v.size(); ++i) {
cout << v[i] << " ";
}
cout << "\n";
}
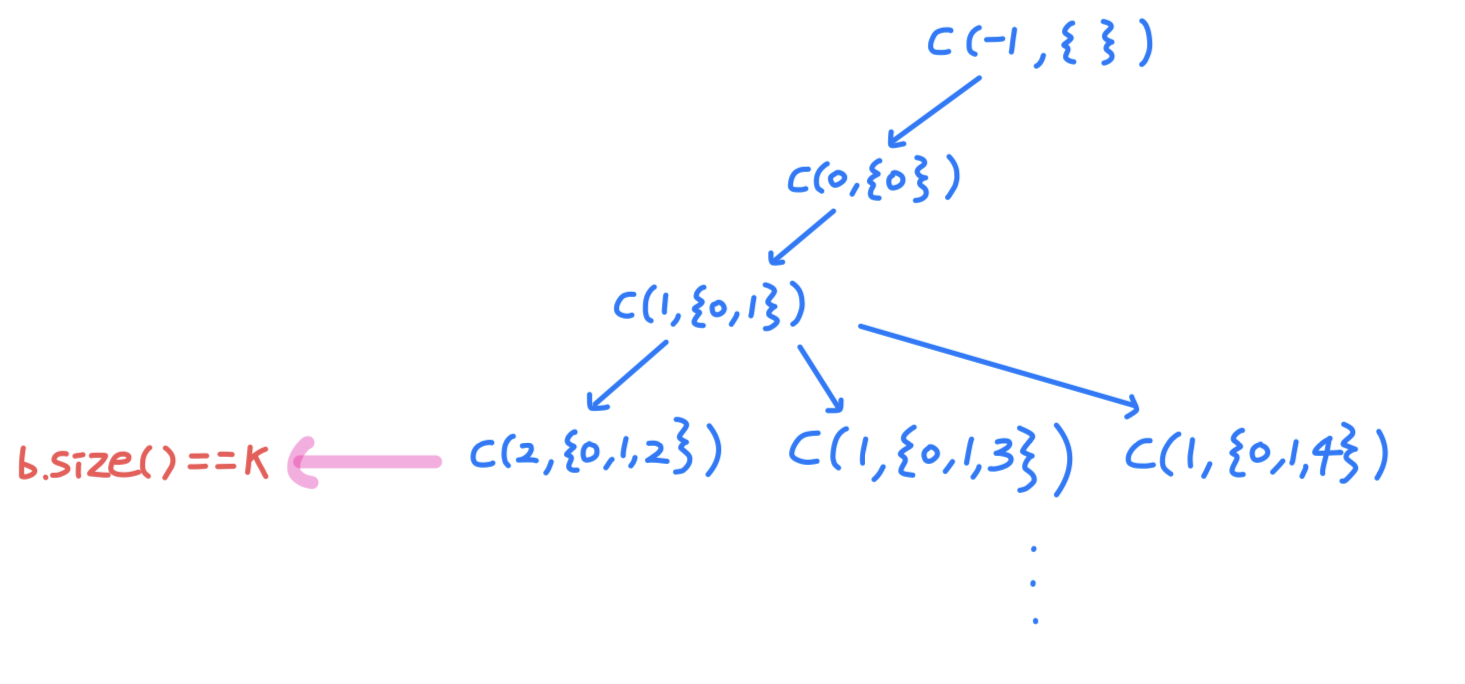
void combi(int start, vector<int> b) {
if (b.size() == k) {
printV(b);
return;
}
for (int i = start+1; i < n; ++i) {
b.push_back(i);
combi(i, b);
b.pop_back();
}
return;
}
int main() {
combi(-1, b);
}
// 0 1 2
// 0 1 3
// 0 1 4
// 0 2 3
// 0 2 4
// 0 3 4
// 1 2 3
// 1 2 4
// 1 3 4
// 2 3 4주의
출력된 결과는 원소가 아니라 index이다.
반복문으로 구현
반복문으로 조합을 구현할 때 0개를 뽑기 위해서는 0중 반복문이 필요하다.
int main() {
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
for (int l = j + 1; l < n; ++l) {
cout << i << j << l << "\n";
}
}
}
}
Reference
10주완성 C++ 코딩테스트 | 알고리즘 코딩테스트 - 인프런 | 강의
네이버, 카카오, 삼성의 코딩테스트를 10주만에 합격시킨 최고의 코딩테스트 강의!, 코딩테스트, 이제 검증된 10주 완성 커리큘럼으로 정복하자!😎 [사진] 코딩테스트 강의어떤 것을 골라야 할까
www.inflearn.com