[BOJ 11657] 타임머신

11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
1. 문제 설명

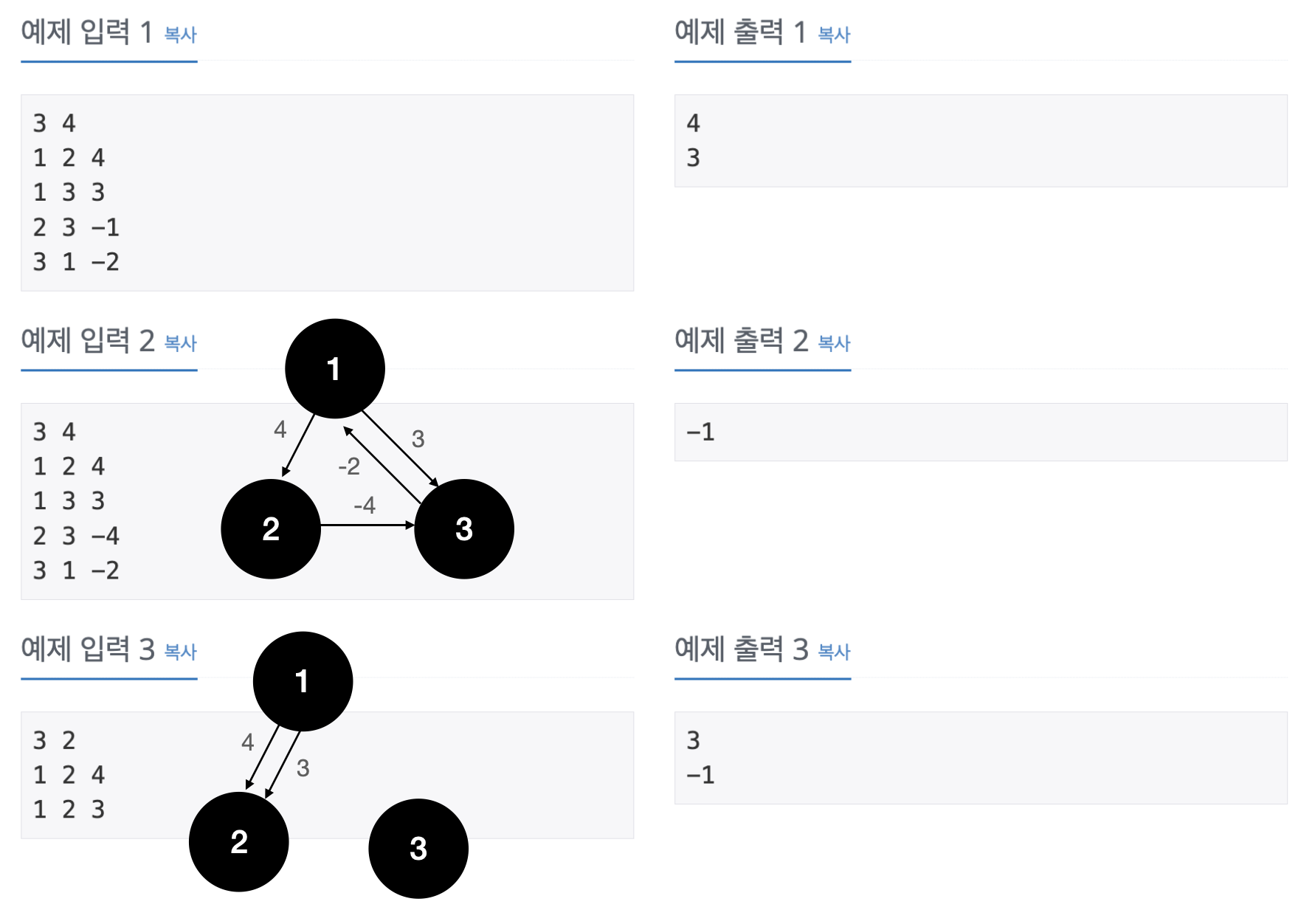
예제 입력 2의 경우 4 > -4 > -2 루프를 반복하면 무한대로 작아지기 때문에 -1을 출력한다.
예제 입력 3의 경우 1번 도시와 3번 도시가 연결되어 있지 않으므로 2번째 줄에 -1을 출력한다.
2. 구현 아이디어 1 - 출력 초과
C < 0인 경우, 즉 음의 간선이 있기 때문에 벨만 포드 알고리즘을 사용한다.
벨만 포드는 음의 간선이 존재할 때 사용하는 최단 거리 알고리즘이다.
1. 최단 거리 테이블 갱신: (정점 - 1)번을 반복하며 매 단계마다 모든 간선을 전부 확인하며 최단 거리를 갱신한다.
2. 음수 간선 순환 확인: 1번 과정을 1번 더 반복한다.
1번 과정을 통해 모든 간선을 확인하면 최단 거리를 구한다.
만약 음수 간선의 순환이 존재한다면 최단 거리를 다시 구했을 때 최단 거리가 갱신(=최단 거리가 더 작아짐)되기 때문에 음수 간선 순환이 있다고 판단할 수 있다.
#include <bits/stdc++.h>
using namespace std;
#define INF 987654321
int n, m; // 도시, 버스 노선
int a, b, c; // 시작 도시, 도착 도시, 이동 시간
map<int, vector<pair<int, int>>> graph;
bool bellmanFord(map<int, vector<pair<int, int>>> &graph, vector<int> &dist, int start) {
dist[start] = 0;
for (int i = 0; i < graph.size(); ++i) {
for (int j = 0; j <= n; ++j) {
if (graph[j].empty()) continue;
for (auto node : graph[j]) {
int next = dist[j] + node.second;
if (dist[node.first] > next) dist[node.first] = next;
}
}
}
for (int j = 1; j <= n; ++j) {
if (graph[j].empty()) continue;
for (auto node : graph[j]) {
int next = dist[j] + node.second;
if (dist[node.first] > next) return false;
}
}
return true;
}
int main(int argc, char** argv)
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
vector<int> dist = vector<int>(n+1, INF);
for (int i = 0; i < m; ++i) {
cin >> a >> b >> c;
graph[a].push_back({b, c});
}
if (bellmanFord(graph, dist, 1)) {
for (int i = 2; i < dist.size(); ++i) {
if (dist[i] >= INF) cout << -1 << endl;
else cout << dist[i] << endl;
}
} else {
cout << -1 << endl;
}
return 0;
}
처음 보는 문구여서 당황했다.
검색을 해본 결과 N=500, M=6,000일 때(최댓값일 때) 음의 사이클이 존재하면 문제가 된다고 한다.
1 > 2 : -10,000
2 > 1 : -10,000
이렇게 사이클이 있을 때 최악의 경우 거리 값이 500 * 6,000 * -10,000가 될 수 있기 때문에 int의 범위를 넘게 된다.
그러므로 거리와 관련된 dist 배열과 next 변수의 자료형을 long long으로 수정해주었다.
2. 구현 아이디어 2 - 틀렸습니다.
그럼에도 불구하고 문제를 맞추지 못했다 !
3 2
2 3 -1
3 2 -2
## My Output
-1
## Correct Output
-1
-1
위와 같은 반례에서 1번 도시에서 2번이나 3번 도시로 가는 간선이 존재하지 않기 때문에 경로를 출력해야 하는데 음의 사이클이 있다고 판단되어 -1을 출력한다.
음의 사이클이 존재하더라도 1번 도시와 연결되어 있지 않다면 해당 도시의 경로를 -1로 출력해야 한다.
그러므로 최단 거리가 INF인지 판단하는 코드를 추가하였다.
4. 구현 아이디어 4 - 맞았습니다!!
#include <bits/stdc++.h>
using namespace std;
#define INF 987654321
int n, m; // 도시, 버스 노선
int a, b, c; // 시작 도시, 도착 도시, 이동 시간
map<int, vector<pair<int, int>>> graph;
bool bellmanFord(map<int, vector<pair<int, int>>> &graph, vector<long long> &dist, int start) {
dist[start] = 0;
for (int i = 0; i < graph.size(); ++i) {
for (int j = 0; j <= n; ++j) {
if (graph[j].empty()) continue;
for (auto node : graph[j]) {
long long next = dist[j] + node.second;
if (dist[j] != INF && dist[node.first] > next) dist[node.first] = next;
}
}
}
for (int j = 1; j <= n; ++j) {
if (graph[j].empty()) continue;
for (auto node : graph[j]) {
long long next = dist[j] + node.second;
if (dist[node.first] == INF) continue;
if (dist[node.first] > next) return false;
}
}
return true;
}