최소 신장 트리(MST, Minimum Spanning Tree) - 크루스칼, 프림 알고리즘

1. 최소 신장 트리란?

신장 트리(Spanning Tree)란 그래프의 모든 노드가 사이클 없이 연결된 부분 그래프를 의미한다. 신장 트리는 여러 개가 존재할 수 있으며, 이 중 모든 노드가 최소 간선의 합으로 연결되었을 때를 최소 신장 트리(MST, Minimum Spanning Tree)라고 한다.

 

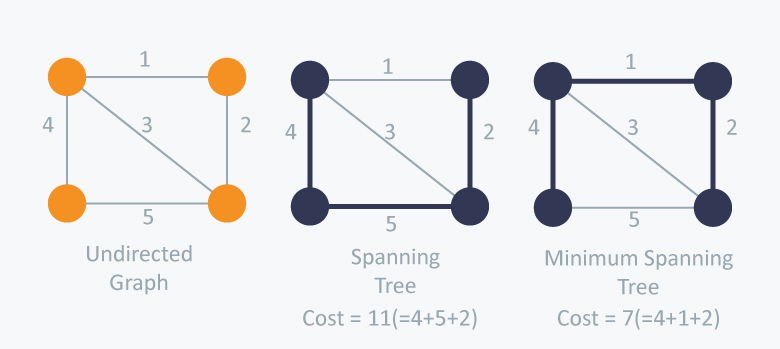
최소 신장 트리를 찾을 수 있는 대표적인 알고리즘 2가지가 있는데, 크루스칼 알고리즘과 프림 알고리즘이다.

크루스칼은 간선 중심, 프림은 정점 중심 알고리즘이다. 정점 대비 간선이 적으면(Sparsh Graph) 크루스칼을, 많으면(Dense Graph) 프림을 사용하는 것이 좋다.

• 크루스칼 알고리즘의 시간복잡도: O(ElogE)
• 프림 알고리즘의 시간복잡도: O(VlogV+ElogV)

둘 다 음의 간선이 있더라도 사용 가능하다.

 

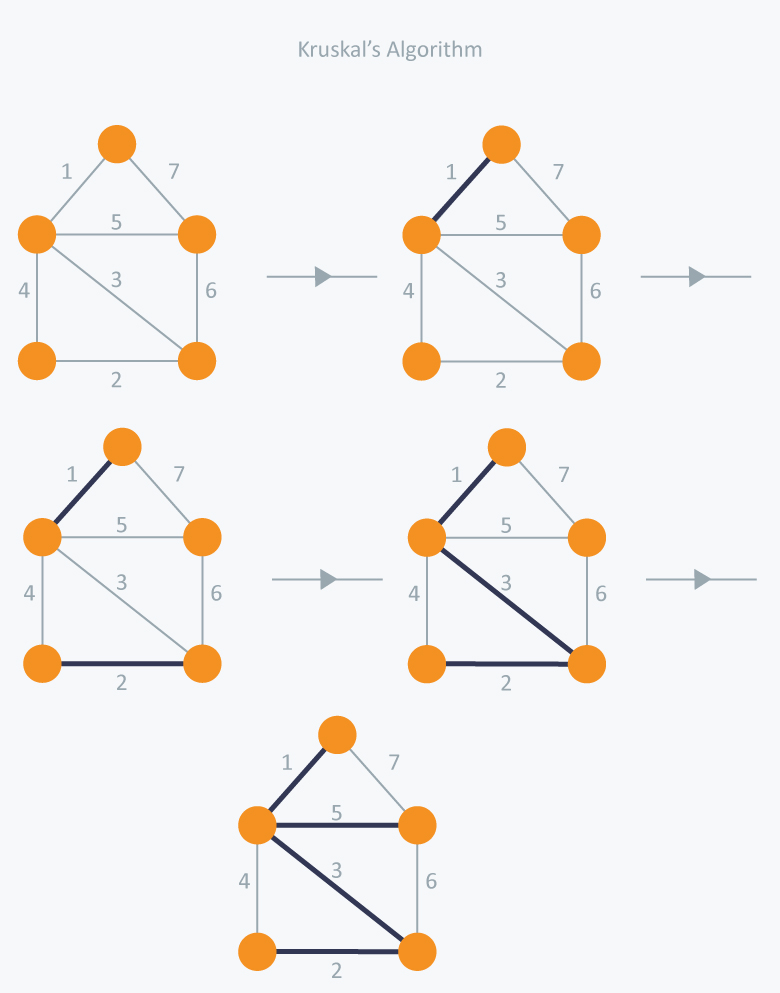
2. 크루스칼 알고리즘 (Kruskal's Algorithm)

1. 간선을 가중치를 기준으로 오름차순으로 정렬한다.
2. 정렬된 간선 중 가장 가중치가 적은 것부터 큰 것을 순차적으로 선택한다.
3. 사이클이 발생하지 않을 경우 MST에 포함하고, 발생한다면 포함하지 않는다.
4. 2번과 3번을 MST 집합(간선의 집합)의 원소가 V-1개가 될 때까지 2, 3을 반복한다. 

 

여기서 3번을 구현하기 위해 유니온 파인드(Union Find) 알고리즘을 사용하면 된다.

유니온 파인드는 두 노드가 같은 집합에 속하는지 판별하는 알고리즘으로, 노드를 합치는 연산인 Union과 루트 노드를 찾는 Find 연산으로 이루어져 있다.

// 루트 노드를 찾는다
int find(int x) {
	if (x==parent[x]) return x;
    
    int p = find(parent[x]);
    parent[x] = p;
    return p;
}

// 두 노드를 하나의 집합으로 합친다
// 루트 노드를 더 작은 값으로 저장
void merge(int a, int b) {
    int A = find(a);
    int B = find(b);
    
    if(A < B) parent[B] = A;
    else parent[A] = B;
}

 

아래 그림을 보면 간선을 작은 것부터 차례대로 고르지만, 4번째 단계에서 4를 선택하면 사이클을 이루기 때문에 5를 선택한다.

 

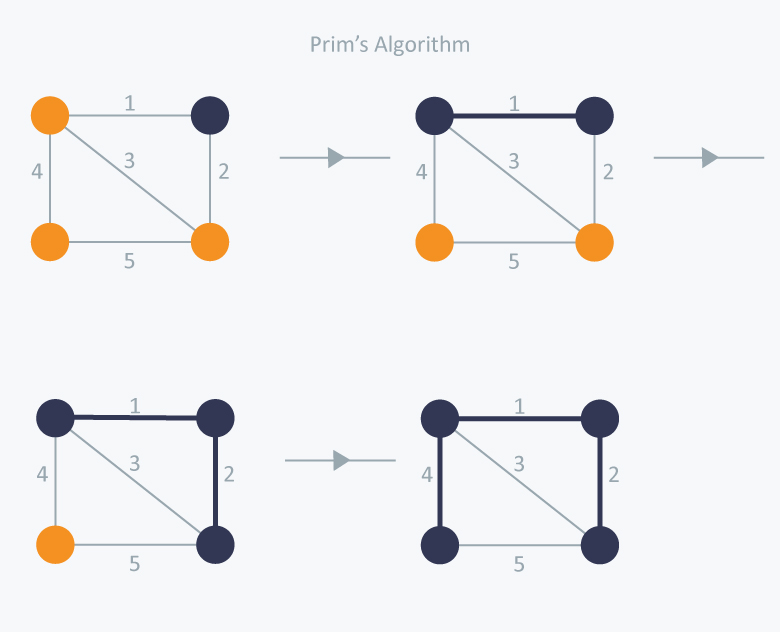
3. 프림 알고리즘 (Prim's Algorithm)

1. 시작 노드를 MST 집합에 포함한다.
2. MST 집합에 속한 정점들과 인접한 노드들 중 방문하지 않았고, 가장 낮은 가중치의 간선과 연결된 노드를 선택한다.
3. 선택한 간선과 노드를 MST 집합에 포함하고 방문 처리한다.
4. MST 집합의 원소의 개수가 V개가 될 때까지 2번과 3번을 반복한다.

 

프림 알고리즘에서는 방문 여부를 저장하므로 이미 방문한 노드를 다시 지나지 않게 되어 사이클을 예방할 수 있다.

프림 알고리즘에서 2번 과정을 구현하기 위해서 우선순위 큐를 사용한다.

 

Reference

https://www.hackerearth.com/practice/algorithms/graphs/minimum-spanning-tree/tutorial/

https://roytravel.tistory.com/348