[C++] 세그먼트 트리의 개념과 구현

1. 세그먼트 트리란?

여러 개의 데이터가 존재할 때 특정 구간의 합(최솟값, 최댓값, 곱 등 ...)을 구하는데 사용하는 자료 구조이다.

트리 종류 중 하나로 이진 트리의 형태이며, 특정 구간의 합을 가장 빠르게 구할 수 있다는 장점이 있다. → O(logN)

 

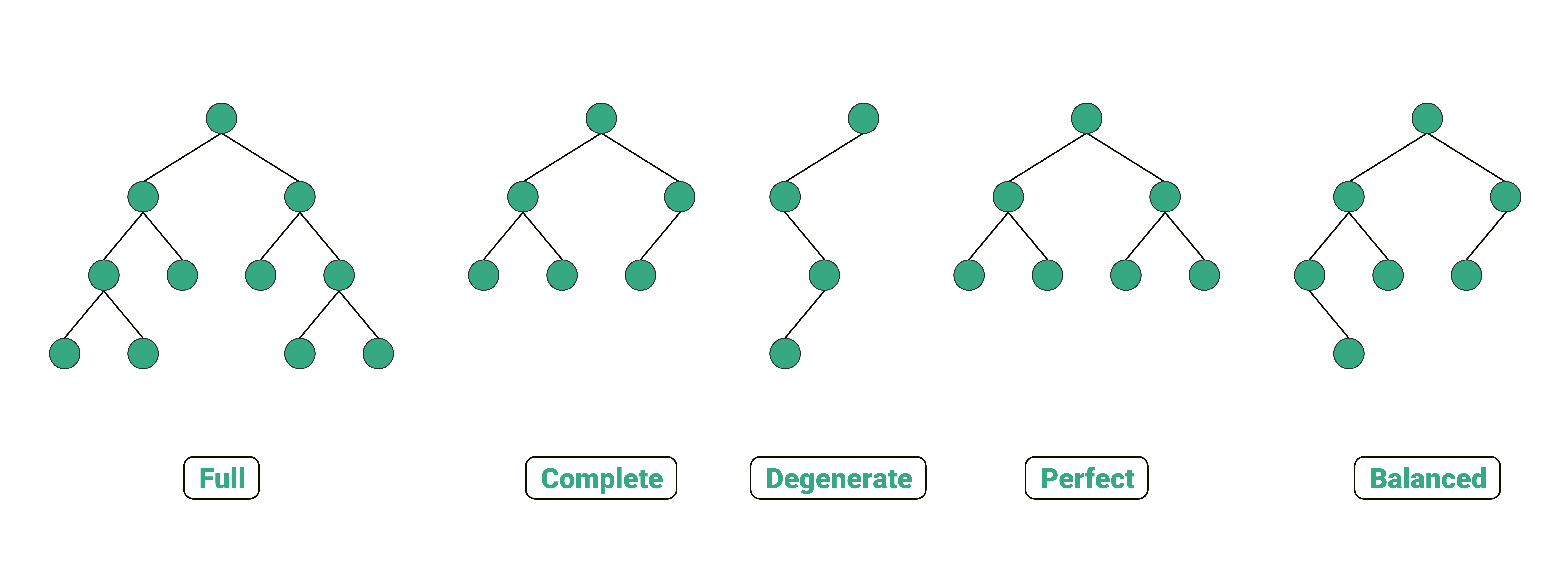
세그먼트 트리는 이진 트리 중에서도 전 이진트리(Full Binary Tree)에 해당한다.

전 이진 트리: 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

이진 트리의 종류

 

2. 세그먼트 트리의 구성

먼저 이진 트리를 구성할 때 루트 노드는 1부터 시작한다. (0부터 시작하면 인덱스 관리가 어렵다)

그 아래부터는 부모 노드의 인덱스를 i라고 할 때 왼쪽 자식 노드는 2i, 오른쪽 자식 노드는 2i+1이 된다.

 

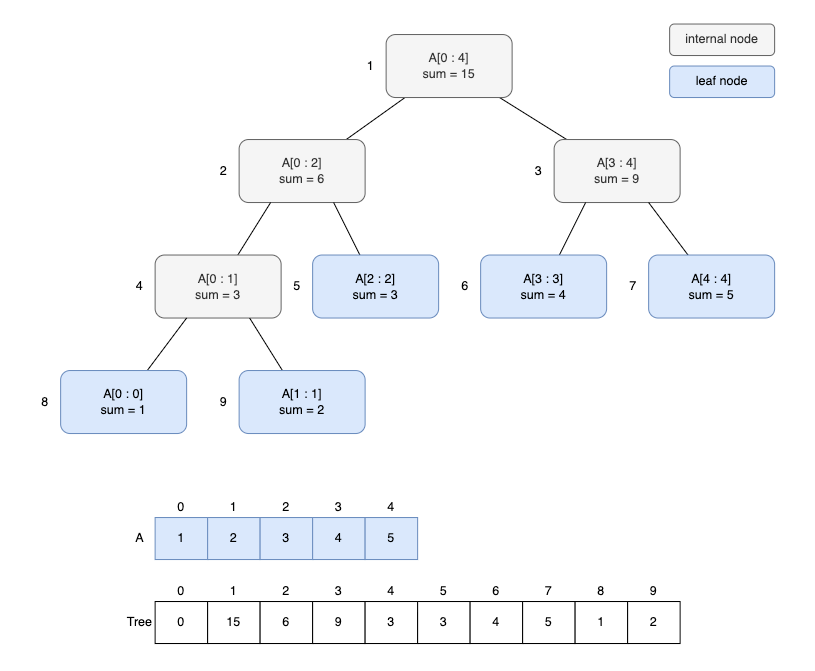
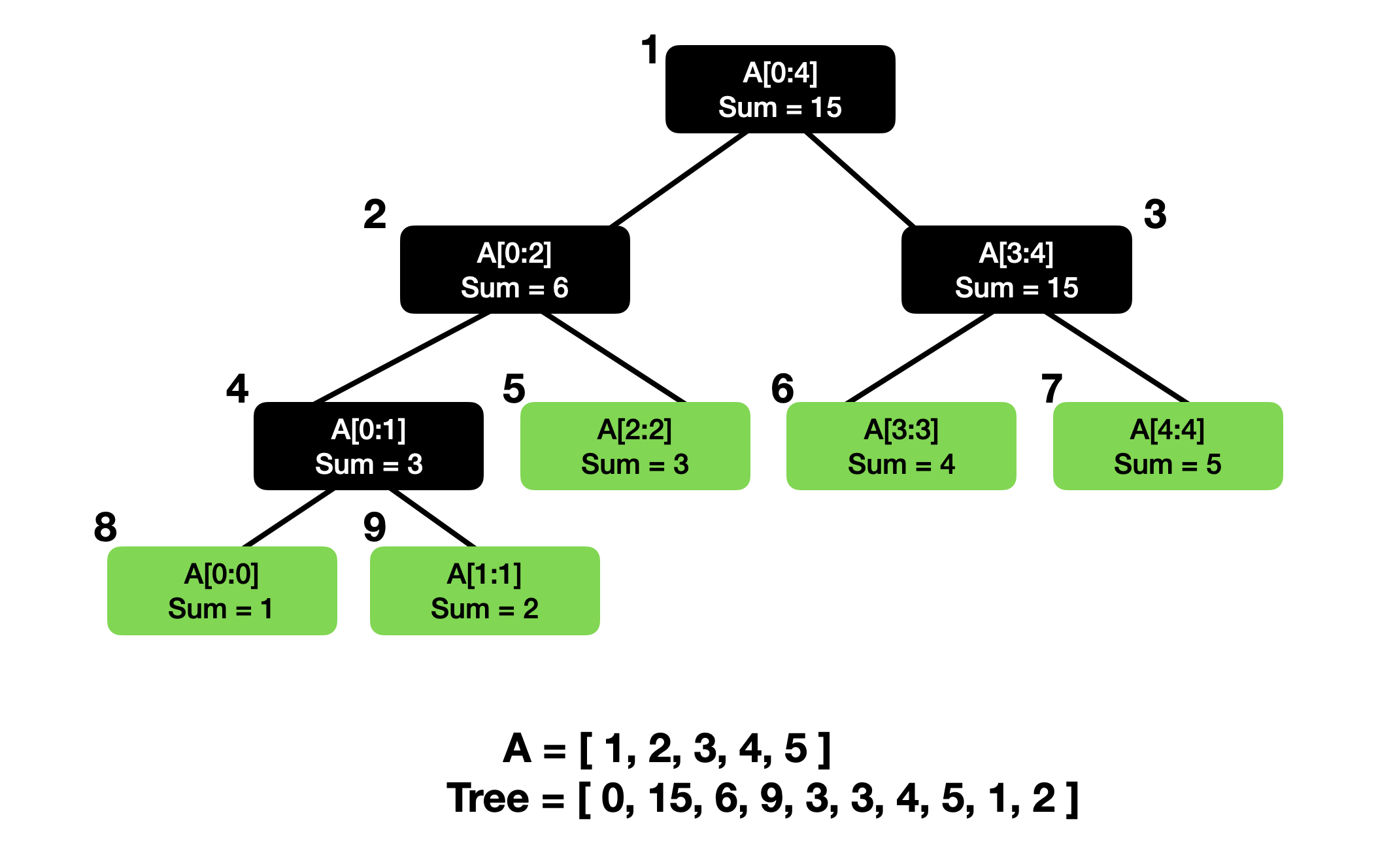
아래는 A={ 1, 2, 3, 4, 5 }라는 배열에 대한 세그먼트 트리를 시각화한 그림이다.

 

각 노드에는 배열의 구간 합이 저장되어 있다.

리프 노드에는 주어진 배열의 값들(A[0], A[1], ...)이, 내부 노드에는 자식 노드의 합이 저장된다.

 

크기가 n인 배열로 리프 노드가 n개인 세그먼트 트리를 만들기 위해서는

높이 h가

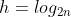
일 때, 필요한 배열의 크기는

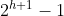
이며, 편의를 위해

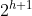
이나 4n으로 크기를 정하기도 한다.

 

int n; // 배열의 원소의 개수
int h = (int) ceil(log2(n)); // 트리의 높이
int treeSize = (1 << (h+1)); // 배열의 크기

 

3. 세그먼트 트리의 구현

세그먼트 트리에는 3가지 기능이 필요하다.

• init - 초기화
• query - 구간합 구하기
• update - 변경

 

3가지 모두 분할 정복을 사용하여 구현한다.

Init (초기화)

리프 노드가 주어진 배열의 값이고, 나머지 내부 노드에서는 부모 노드가 자식 노드의 합이 된다.

재귀에서 탈출 조건은 현재 노드가 리프 노드일 때, 즉 start와 end가 같을 때이다.

ll init(vector<ll> &arr, vector<ll> &tree, int node, int start, int end) {
    // 노드가 리프 노드인 경우
    if (start == end) return tree[node] = arr[start];

    int mid = (start + end) / 2;

    // 구간 합을 구하는 경우
    // 부모 노드 = 왼쪽 자식 노드 + 오른쪽 자식 노드
    return tree[node] = init(arr, tree, node * 2, start, mid) + init(arr, tree, node * 2 + 1, mid + 1, end);

    // 구간의 최솟값을 구하는 경우
    // return tree[node] = min(init(arr, tree, node * 2, start, mid), init(arr, tree, node * 2 + 1, mid + 1, end));
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int n = 5; // 배열의 원소의 개수
    vector<ll> arr = {1, 2, 3, 4, 5};

    int h = (int) ceil(log2(n)); // 트리의 높이
    int treeSize = (1 << (h+1)); // 배열의 크기
    vector<ll> tree(treeSize); // 세그먼트 트리 생성

    // 세그먼트 트리 초기화
    init(arr, tree, 1, 0, n-1);

    return 0;
}

 

 

2. 세그먼트 트리의 구성과 동일한 배열로 예제를 만들었을 때, 아래와 같이 세그먼트 트리가 정상적으로 초기화된 것을 확인할 수 있다.

 

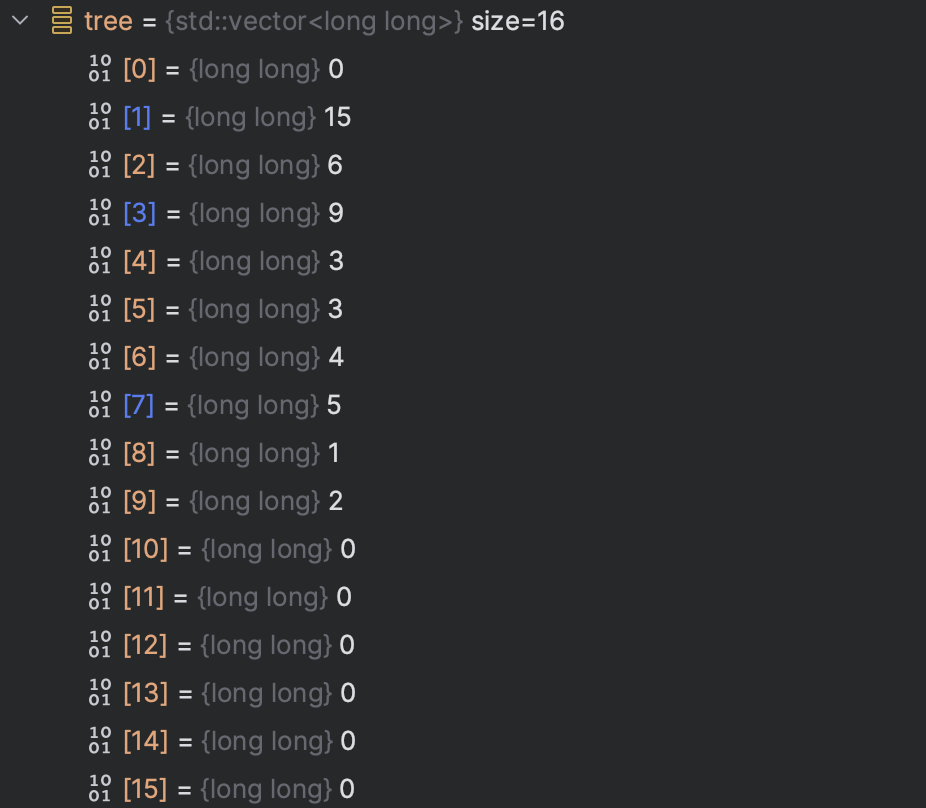
Query (구간 합 구하기)

구간 [left, right]이 주어졌을 때 구간 합을 찾기 위해서는 각 노드가 담당하는 구간 [start, end]와 [left, right] 사이의 관계를 고려해야 한다.

 

예를 들어, 0번째부터 4번째 원소의 합은 루트 노드 하나만으로 알 수 있다.

 

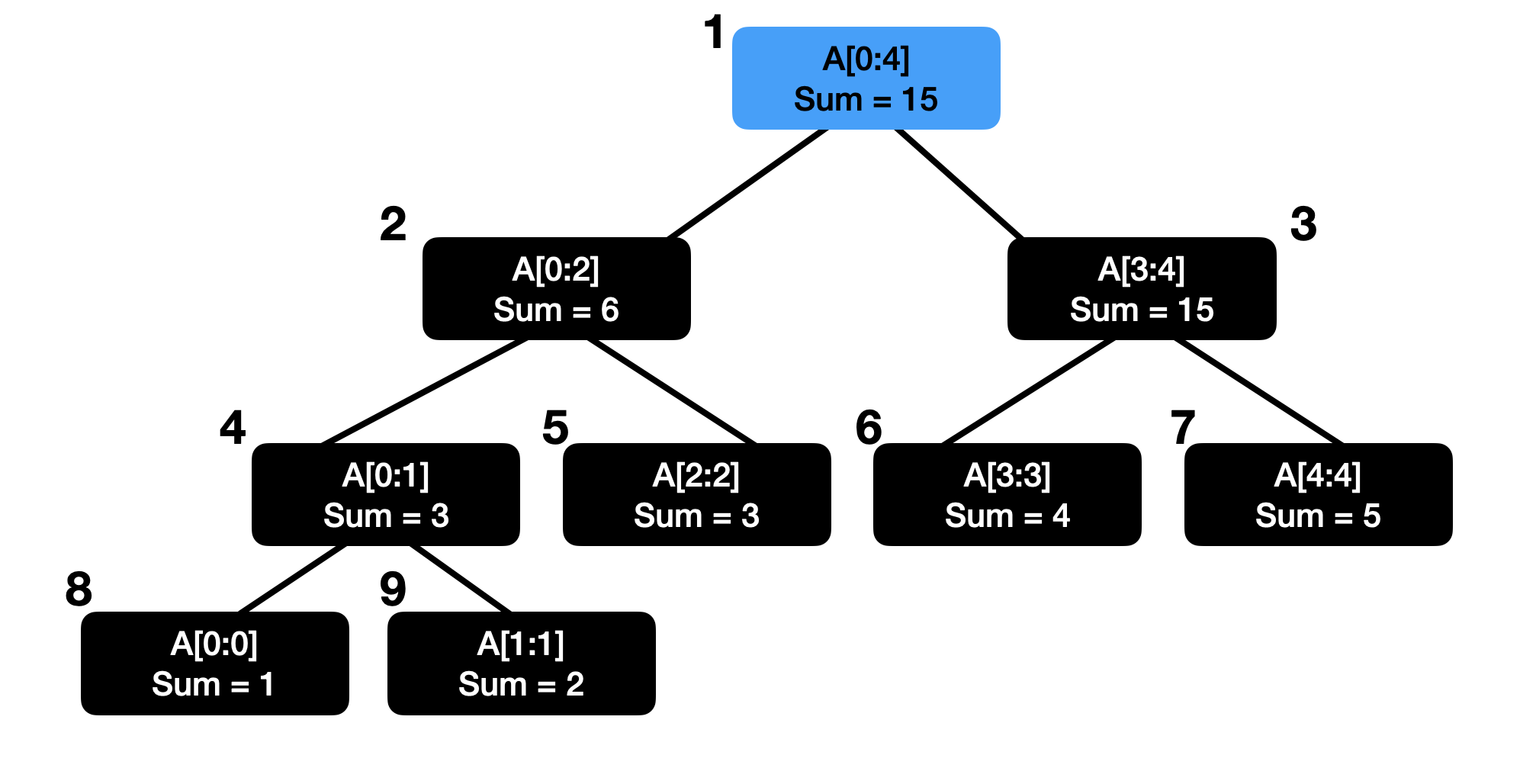
그리고 2번째~4번째 원소의 구간 합은 3번 노드와 5번 노드의 합으로 구할 수 있다.

 

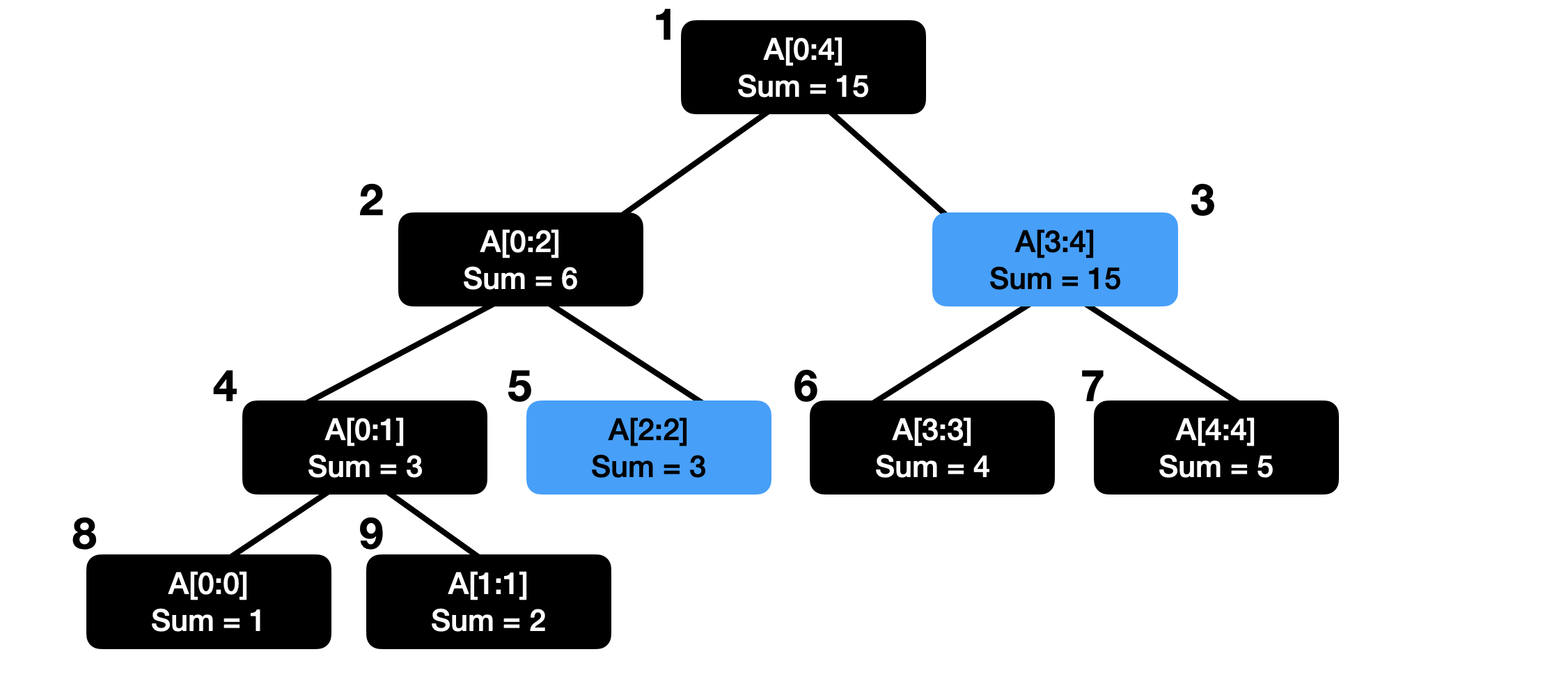
구간 합을 구할 때는 4가지 경우로 나눠서 생각할 수 있다.

1. [left, right]이 [start, end] 범위 내에 없을 경우
2. [left, right]가 [start, end]를 완전히 포함하는 경우
3. [start, end]가 [left, right]을 완전히 포함하는 경우
4. [left, right]와 [start, end]가 겹쳐 있는 경우

ll query(vector<ll> &tree, int node, int start, int end, int left, int right) {
    // case 1: [start, end] 범위 안에 [left, right]가 없는 경우
    // 재귀 종료
    if (left > end || right < start) return 0;

    // case 2: [left, right]가 [start, end]를 완전히 포함
    if (left <= start && end <= right) return tree[node];

    // case 3, 4: 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색 시작
    int mid = (start + end) / 2;
    ll leftChild = query(tree, node*2, start, mid, left, right);
    ll rightChild = query(tree, node*2+1, mid+1, end, left, right);
    return leftChild + rightChild;
}

 

Update (수 변경하기)

중간에 어떤 수를 변경하면, 해당 숫자가 포함된 구간을 담당하는 노드를 모두 변경해주어야 한다.

 

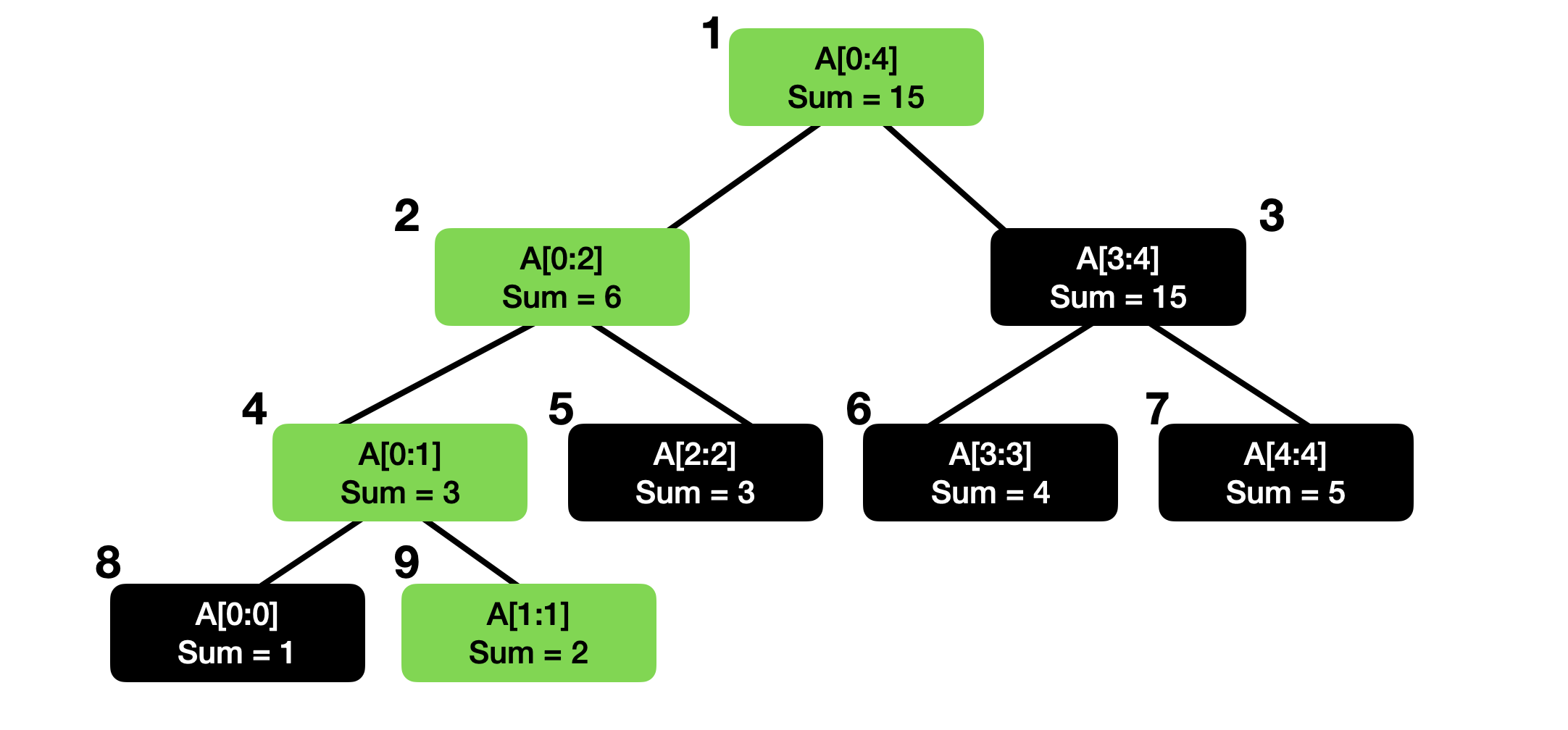
만약 1번째 원소를 변경해준다면 트리에서 해당 원소가 포함된 구간을 의미하는 1, 2, 4, 9번 노드를 변경해주어야 한다.

 

void update(vector<ll> &tree, int node, int start, int end, int index, ll diff) {
    // case 1: [start, end]와 [left, right]이 겹치지 않는 경우
    if (index < start || index > end) return;

    // case 2: [start, end]가 [left, right]에 포함
    tree[node] = tree[node] + diff;

    // 리프 노드가 아닌 경우에는 자식 노드도 변경해주어야 함
    if (start != end) {
        int mid = (start + end) / 2;
        update(tree, node*2, start, mid, index, diff);
        update(tree, node*2+1, mid+1, end, index, diff);
    }
}

 

노드의 구간에 포함되는 경우, diff만큼 값을 증가시켜 트리에서 합을 변경해준다.

 

전체 코드 (예제 포함)

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

ll init(vector<ll> &arr, vector<ll> &tree, int node, int start, int end) {
    // 노드가 리프 노드인 경우
    if (start == end) return tree[node] = arr[start];

    int mid = (start + end) / 2;

    // 구간 합을 구하는 경우
    return tree[node] = init(arr, tree, node * 2, start, mid) + init(arr, tree, node * 2 + 1, mid + 1, end);

    // 구간의 최솟값을 구하는 경우
    // return tree[node] = min(init(arr, tree, node * 2, start, mid), init(arr, tree, node * 2 + 1, mid + 1, end));
}

ll query(vector<ll> &tree, int node, int start, int end, int left, int right) {
    // case 1: [start, end] 앞 뒤에 [left, right]가 있는 경우
    if (left > end || right < start) return 0;

    // case 2: [start, end]가 [left, right]에 포함
    if (left <= start && end <= right) return tree[node];

    // case 3, 4: 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색 시작
    int mid = (start + end) / 2;
    return query(tree, node*2, start, mid, left, right) + query(tree, node*2+1, mid+1, end, left, right);
}

void update(vector<ll> &tree, int node, int start, int end, int index, ll diff) {
    // case 1: [start, end]와 [left, right]이 겹치지 않는 경우
    if (index < start || index > end) return;

    // case 2: [start, end]가 [left, right]에 포함
    tree[node] = tree[node] + diff;

    // 리프 노드가 아닌 경우에는 자식 노드도 변경해주어야 함
    if (start != end) {
        int mid = (start + end) / 2;
        update(tree, node*2, start, mid, index, diff);
        update(tree, node*2+1, mid+1, end, index, diff);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int n = 5; // 배열의 원소의 개수
    vector<ll> arr = {1, 2, 3, 4, 5};

    int h = (int) ceil(log2(n)); // 트리의 높이
    int treeSize = (1 << (h+1)); // 배열의 크기
    vector<ll> tree(treeSize); // 세그먼트 트리 생성

    cout << "세그먼트 트리 배열의 길이: " << treeSize << endl;

    // 세그먼트 트리 초기화
    init(arr, tree, 1, 0, n-1);

    // [1, 3] 구간 합 출력
    int left = 1, right = 3;
    ll result = query(tree, 1, 0, n-1, left, right);
    cout << "[" << left << ", " << right << "]의 구간 합: " << result << endl;

    // 2번 인덱스 값을 5로 업데이트
    int index = 2;
    ll diff = 5 - arr[index];
    update(tree, 1, 0, n-1, index, diff);

    // [1, 3] 구간 합 다시 출력
    result = query(tree, 1, 0, n-1, left, right);
    cout << "[" << left << ", " << right << "]의 구간 합: " << result << endl;

    return 0;
}

 

4. 시간 복잡도

각 함수의 사건 복잡도는 아래와 같다.

기능	시간 복잡도
init	O(N), 노드의 수와 동일
query	O(logN)
update	O(logN)

 

Reference

세그먼트 트리(Segment Tree) 개념 및 구현

 

[자료구조] 세그먼트 트리 (Segment Tree) C++ 구현